
This is the first part of our two-part privacy tech-know blog series on algorithmic fairness. In this first part, we will introduce the topic of algorithmic fairness and analyze the three main definitions of it, listing the pros and cons of each as well as describing the different trade-offs between definitions. In the second part, we will further develop our analysis by focusing on topics more specific to the practical side of algorithmic fairness. Throughout this discussion, we assume working-level technical knowledge of artificial intelligence (AI) and machine learning (ML).
Introduction
Fairness is a fundamental concept of ethics. It has a long history, dating back to at least the ancient Greeks, whose philosophical studies made a number of important insights into the nature of it. One is that fairness, like all virtues, has a peculiar ambiguity to it. It is not like mathematics or the natural sciences, whose laws are incapable of being otherwise—or at least aim to be. When we decide whether some course of action is fair (or unfair), the standard we use is variable and subject to change, especially over time.
The reason for this variability has to do with the nature of ethical thinking. Whereas mathematics and the natural sciences use calculation to derive their results, fairness works through a process of deliberation. Deliberation is fundamentally different from calculation. What distinguishes it is its full sense of temporality. When we deliberate, we do not simply view the facts of a scenario through the lens of the past or the present, in the sense of the way the world was or currently is. Even more so, we look to the future, in the sense of the way we want the world to be.
The Greek philosopher Aristotle (384–322 BC) had a nice way of expressing this future-oriented ambiguity of fairness. He said that ethical human action takes the form of a mean between two extremes.Footnote 1 Today, this insight is often expressed in less philosophical terms. We say that whether something is fair (or unfair) depends on the circumstances.
In contrast to fairness, AI, including its sub-discipline of ML, is a more recent phenomenon. Both the terms “artificial intelligence” and “machine learning” originated in the 1950s.Footnote 2 Despite some periods of reduced funding and skepticism, the field has progressed significantly, with research in the 21st century proving especially productive. During this time, advancements in computer processing and neural network architectures led to the establishment of the further sub-discipline of “deep learning.”Footnote 3
AI/ML is a modern mathematical technology. It emulates human tasks by representing them in the form of a complex statistical model. Key to AI/ML is the idea of “learning through examples.” In general, AI/ML learns by tuning the parameters of a statistical model to best fit the features of some example training data in order to minimize the value of a cost function.
When compared to the ethical concept of fairness, AI/ML exhibits an opposite set of characteristics. Instead of a type of productive ambiguity, its mode of work is determined by the precision of mathematics. During development, it uses the optimization methods of calculus to refine the slope and direction by which to tune the parameters of its model. During deployment, it applies the learned model to new examples to calculate their results.
Moreover, the perspective it brings to a given situation is not open to the future but remains focused on the past. When evaluating new examples, AI/ML is constrained in its perspective to the standpoint represented by the training, evaluation and test data used to develop it. While this static horizon is what enables AI/ML to emulate human tasks with the speed and repeatability of an algorithm, it also brings with it an important limitation. Unlike ethical thinking, AI/ML cannot interpret new examples against a meaningful world of future possibilities. Instead, like the famous Shakespeare quote, “What’s past is prologue.”Footnote 4
So, what happens when these two worlds collide? What happens, in other words, when the future-oriented ambiguity of fairness meets the past-is-prologue precision of AI/ML? The result is an emerging field of research called “algorithmic fairness.”
Ensuring algorithmic fairness is a pressing concern for society today. As our reliance on AI/ML grows and as the number of areas in which AI/ML is applied increases, the question of whether our uses of it are compatible with the idea of a fair and just society becomes more urgent.
As an interdisciplinary field of study, algorithmic fairness raises both philosophical questions and technical considerations. For example, what is the meaning of fairness as such? What does fairness mean within the context of AI/ML? What is the relationship between definitions of algorithmic fairness? What measures can be taken to help achieve it? Are there limits to such mathematical notions of fairness?
In this two-part blog series, we will explore some key aspects of algorithmic fairness in the hopes of shedding light on both its possibilities and limits. To clarify, this document does not provide guidance on the application of algorithmic fairness under federal privacy laws. The aim of this first part is to analyze the main definitions of algorithmic fairness to help contextualize our understanding of it from a technical perspective, as opposed to a legal or policy perspective.
What is fairness?
Before jumping into a discussion of algorithmic fairness, it is helpful to say a few words about the ethical concept of fairness as such. As a type of fairness, algorithmic fairness shares in the basic properties of fairness, which is its “genus.” While its connection to AI/ML is what defines it more specifically, its origins nonetheless lie in the ethical concept of fairness. Thus, a good first step towards understanding it as a whole is to explore the idea of fairness.
Once again, Aristotle can help us. His philosophical works on ethics and politics attempt to uncover the essential conditions under which human co-existence must take place to reach a form that is self-sustaining and complete. Fairness is one of those conditions.
Aristotle defines fairness in multiple ways, but the definition most applicable to our discussion of algorithmic fairness is the one he provides in his study of different forms of government. There, Aristotle remarks (paraphrase):
Everyone agrees that fairness [or “justice”; to dikaion] involves treating equal persons equally, and unequal persons unequally, but they do not agree on the standard by which to judge individuals as being equally (or unequally) worthy or deserving.Footnote 5
This definition contains three key insights into the nature of fairness as such:
- It involves recognition of both similarities and differences. Fairness is not necessarily sameness of treatment across all individuals or groups. It may also incorporate differences, so long as they can be justified as legitimate departures from strict equality. Ultimately, there are multiple respects in which individuals or groups may be considered similar or different. Fairness recognizes and respects both these elements as essential to achieving the right amount of proportionality in human interactions.
- It has multiple standards. There is no single universal set of criteria against which to measure a situation for compatibility with fairness. Multiple standards of similarities and differences are possible. Of course, not all standards are appropriate and some may even change over time to take account of shifting norms and values. Yet, this inherent ambiguity is not a defect. Quite the contrary. It is what gives fairness the ability to “see” what is right in the circumstances by transcending the status quo of the past while remaining open to the future.
- The standards are generally incompatible. Sameness and difference are fundamental categories of thinking. For this reason, any approach to them that satisfies one standard of fairness will generally conflict with the criteria of other approaches. While multiple standards are possible and may even be equally valid in certain cases, it is difficult, if not impossible, to satisfy them all simultaneously. Ultimately, whether a given standard is appropriate or not is a complex issue, combining legal, social and ethical considerations.
What is algorithmic fairness?
Algorithmic fairness is a type of fairness that arises primarily within the context of an AI/ML model used for classification. Classification is one type of AI/ML task. Others include clustering, transcription, anomaly detection and machine translation. Algorithmic fairness can be used to assess the fairness of these other AI/ML tasks to the extent that their results can be interpreted as a form of classification.
An AI/ML classifier is essentially a model that labels things as belonging to different categories or “buckets.” The label is a prediction. It is typically derived from a real-valued score the model generates that is then thresholded at some cut-off value to determine the numerical range of the category. This makes classification closely related to the task of regression. Regression is like classification, except that the prediction remains in the form of a real-valued score or probability. Many AI/ML classification tasks are trained as regression tasks, and then add a threshold afterwards to define category boundaries.
Algorithmic fairness focusses on three variables that arise within the context of an AI/ML classifier:
- Y, the ground truth or target variable to be predicted
- R, the score or predicted label outputted by the model
- A, the sensitive attribute that defines group membershipFootnote 6
Depending on the relationship between these variables, different definitions of algorithmic fairness are possible. In general, there are three main definitions to consider: sufficiency, separation and independence.
In what follows, we will provide a brief description of each definition, followed by a discussion of its pros and cons. We will generally assume a binary classifier that labels individuals as belonging to one of two categories: a “positive” and a “negative” class. Although simplified, the definitions and insights we obtain in this way can be easily extended to more complex, multiclass models.
Sufficiency
Historically, this is the oldest definition of algorithmic fairness. It was first introduced by Cleary in 1966 in her report on the fairness of the scholastic aptitude test (SAT) as a predictor of college outcomes in the U.S.Footnote 7
Formally, an AI/ML model satisfies sufficiency when, for any predicted score R, the probability of actually belonging to the positive or negative class (as indicated by the ground truth Y) is the same across all groups A. In mathematical notation, this is often expressed as “Y ⊥ A | R,” meaning that the ground truth Y is independent of group membership A given a predicted score R.
The intuition behind sufficiency is that R is meant to be a predictor of Y; thus, an AI/ML model is fair if R does not systematically over- or under-predict Y for members of any group. In other words, the predictions of a fair AI/ML model should be “equally calibrated,” such that R scores map to similar Y values regardless of group membership. If we assume a normal distribution, then sufficiency is equivalent to the situation where the best-fit regression line of Y on R is the same across all groups, that is, the line has the same slope and intercept. More generally, it is equivalent to ensuring a parity of positive and negative predictive values across all groups.
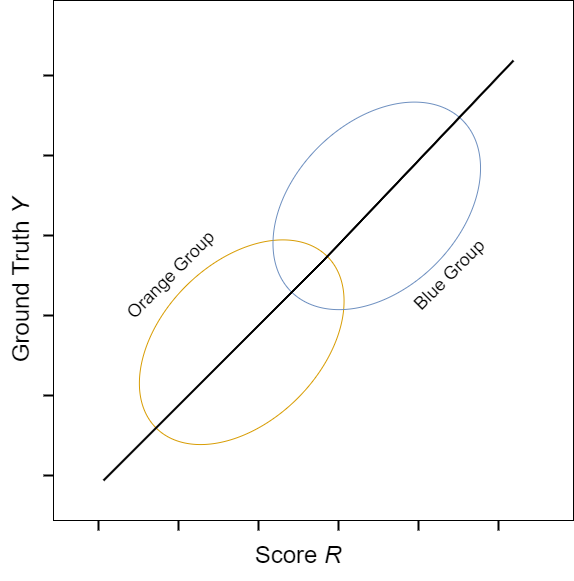
Text version of Figure 1
Figure 1: Example of an AI/ML regression model that satisfies sufficiency. The image depicts an X-Y scatter plot, with the score R plotted on the X-axis and the ground truth Y plotted on the Y-axis. The graph shows data from two groups: an orange group and a blue group. The common regression line runs through the middle of both plots. The model therefore equally calibrates predictions of the target variable for the orange and blue group.
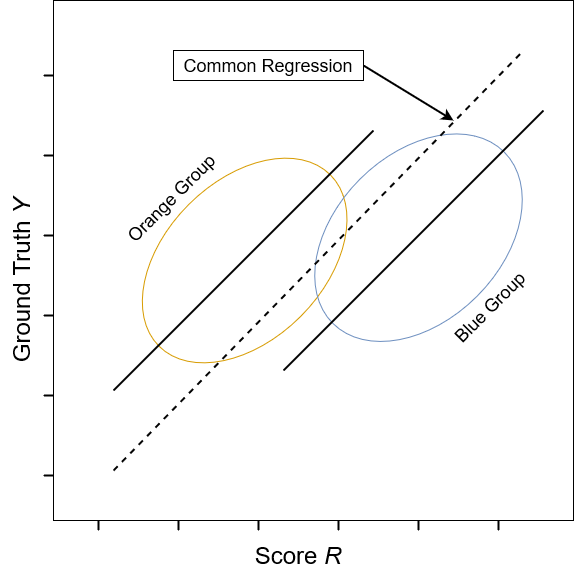
Text version of Figure 2
Figure 2: Example of an AI/ML regression model that does not satisfy sufficiency. The image depicts an X-Y scatter plot, with the score R plotted on the X-axis and the ground truth Y plotted on the Y-axis. The graph shows data from two groups: an orange group and a blue group. The common regression line lies below the plot of the orange group and above the plot of the blue group. The model therefore systematically over-predicts the target variable for the blue group and under-predicts the target variable for the orange group.
The advantage of sufficiency is that it maximizes the predictive validity or overall accuracy of the AI/ML model. The R scores produced by the model will correspond with the highest possible average Y values or fraction of actual positive cases, thereby maximizing the number of correct predictions. In other words, the features within the AI/ML model will fit as closely as possible to the underlying structure of the data given the cost function. Thus, organizations employing an AI/ML model that satisfies the fairness criteria of sufficiency can have confidence that the model closely represents the actual structure of the data.
However, the disadvantage of sufficiency is that it allows an AI/ML model to embed forms of discrimination within its features, so long as the discrimination results in an equal calibration of R and Y values across all groups. For example, if one group receives systematically lower (or higher) R scores than another group, but the structural fit of the AI/ML model is similar for each, then the AI/ML model would continue to meet the fairness criteria of sufficiency, despite the fact that its features are highly correlated with group membership. This opens the door to potential abuse, where group membership is used inappropriately as a proxy for the target variable:
The mind boggles at the vision of a private school using an admissions “test” so culture-bound that it in effect automatically admits all whites and automatically rejects all blacks, with its principal admitting to a low correlation between race and academic aptitude, and yet pointing out that the test is culturally fair by what is currently the most widely accepted definition of cultural fairness.Footnote 8
Separation
Formally, an AI/ML model satisfies separation when, for actual cases of the positive or negative class (as indicated by the ground truth Y), the probability of being correctly or incorrectly assigned to the class (based on the predicted score R) is the same across all groups A. In mathematical notation, this is often expressed as “R ⊥ A | Y,” meaning that the predicted score R is independent of group membership A given a ground truth Y.
The intuition behind separation is that the causal relationship between R and Y can be reversed. Instead of R being a predictor of Y, it is possible to think of Y as an ability that influences R along with A; thus, an AI/ML model is fair only if the probability of selection (or rejection) based on R is uncorrelated with group membership in a subset of people with the same Y outcome. In other words, a fair AI/ML model should produce a state of “equalized odds,” such that group membership A has no direct effect on an individual’s score R given their ground truth Y. This is equivalent to ensuring that all groups experience the same false positive rate and the same false negative rate.
A possible relaxation of the criteria of separation is when only the false negative rate is the same across groups, but not necessarily the false positive rate. Assuming that membership in the positive class is the “advantaged” outcome, this is referred to as “equal opportunity.”Footnote 9
| Blue Group | Orange Group | |||
|---|---|---|---|---|
| Actual – Positive | Actual – Negative | Actual – Positive | Actual – Negative | |
| Predicted – Positive | 45 | 2 | 5 | 18 |
| Predicted - Negative | 45 | 8 | 5 | 72 |
| Total | 90 | 10 | 10 | 90 |
| Error rates | False negative rate: 45 / 90 = 50% False positive rate: 2 / 10 = 20% |
False negative rate: 5 / 10 = 50% False positive rate: 18 / 90 = 20% |
||
| Proportion positive | (45 + 2) / 100 = 47% | (5 + 18) / 100 = 23% | ||
The advantage of separation is that it encourages the AI/ML model to prioritize features that directly predict the target variable, without indirectly relying on group membership as a proxy for Y. The R scores produced by the model will result in a state of “equalized odds,” where individuals with the same Y outcome receive the same probability of selection (or rejection) regardless of group membership. In effect, this prohibits an AI/ML model from embedding forms of potential discrimination within its features. Thus, organizations employing an AI/ML model that meets the fairness criteria of separation can have confidence that the model is not inappropriately influenced by group membership.
However, the disadvantage of separation is that it may reduce the accuracy of the AI/ML model in cases where group membership actually correlates with the target variable. This occurs when base rates of membership in the positive or negative class differ between groups. In such cases, explicitly discouraging the AI/ML model from picking up and learning such correlations may lead to R scores that systematically over- or under-predict the target variable for some groups. For example, studies have shown that rates of recidivism for women are considerably less than those for men.Footnote 10 Not recognizing or suppressing this correlation may lead to an AI/ML model that overestimates women’s likelihood to recidivate.Footnote 11
Independence
Formally, an AI/ML model satisfies independence when, regardless of actual cases of the positive or negative class (as indicated by the ground truth Y), the probability of being assigned to the positive class (based on the predicted score R) is the same across all groups A. In mathematical notation, this is often expressed as “R ⊥ A,” meaning that the predicted score R is independent of group membership A regardless of ground truth Y.
The intuition behind independence is a belief that ultimately the demographics of the population as a whole should act as the ground truth for an AI/ML model, that is, the predictions of an AI/ML model should be “independent” of the ground truth. Thus, an AI/ML model is fair only if it assigns the same proportion of members from each demographic group to the positive or negative class, regardless of the actual proportion of cases in each. In other words, even if there are differences in base rates across groups, the AI/ML model should act as if no such correlation between group membership and the target variable exists. This is equivalent to the idea of “statistical parity.”
| Blue Group | Orange Group | |||
|---|---|---|---|---|
| Actual – Positive | Actual – Negative | Actual – Positive | Actual – Negative | |
| Predicted – Positive | 31 | 1 | 8 | 24 |
| Predicted - Negative | 59 | 9 | 2 | 66 |
| Total | 90 | 10 | 10 | 90 |
| Error rates | False negative rate: 59 / 90 = 66% False positive rate: 1 / 10 = 10% |
False negative rate: 2 / 10 = 20% False positive rate: 24 / 90 = 27% |
||
| Proportion positive | (31 + 1) / 100 = 32% | (8 + 24) / 100 = 32% | ||
The advantage of independence is its simplicity. If the target variable does not correlate with group membership, then neither should the proportion of predicted scores outputted by the AI/ML model. In effect, independence assumes that the target variable is a universal attribute shared by everyone. Thus, organizations employing an AI/ML model that meets the fairness criteria of independence can have confidence that the model ensures an equalization of outcomes across groups.
However, the disadvantage of independence is that it introduces a form of discrimination against individuals in cases where base rates differ across groups.Footnote 12 The AI/ML model will incorrectly select a lower proportion of actual positive cases from groups with higher base rates and a higher proportion of actual negative cases from groups with lower base rates. In effect, this means an increase in false negatives for groups with higher base rates and an increase in false positives for groups with lower base rates. For example, in Table 2, the overall proportion of positive predictions is the same (32%) across both the blue and orange group, thereby satisfying independence. However, the base rate of individuals in the positive class differs. For the blue group, it is 90% (90/100), whereas for the orange group, it is 10% (10/100). Consequently, 66% (59/90) of qualified individuals in the blue group are incorrectly assigned to the negative class, compared with 20% (2/10) in the orange group.
What is the relationship between definitions?
Based on the above discussion, it should be clear that the three main definitions of algorithmic fairness are generally incompatible with each other. Despite each providing a standard of fairness for AI/ML classifiers, they cannot be satisfied simultaneously, except in highly constrained special cases with trivial solutions.
Formal proofs are available to show this.Footnote 13 However, conceptually, the incompatibility is as follows:
- Sufficiency maximizes accuracy by not trying to minimize differences among groups
- Separation minimizes differences among groups by not trying to maximize accuracy
- Independence assumes no differences among groups, regardless of accuracy
In practice, this relationship between definitions amounts to a trade-off between maximizing accuracy and minimizing differences among groups. In general, the more a definition of algorithmic fairness maximizes the accuracy of the AI/ML model, the less it is able to minimize the effects of different base rates across groups, and vice-versa.
The deeper reason for this incompatibility lies in the fact that each definition embeds a different interpretation of sameness and difference with respect to individuals. Sufficiency thinks of sameness only in terms of the predictive validity of the AI/ML model, whereas independence thinks of sameness only in terms of base rates across groups. As a result, sufficiency allows for differences among groups, but independence does not. The perspective of separation lies somewhere in the middle.
Despite their general incompatibility, it is possible for some or all of the definitions to be satisfied simultaneously. However, the solution space that enables compatibility lies at the margins of the trade-off between maximizing accuracy and minimizing differences among groups. For this reason, the conditions are difficult to obtain in practice, but even when they are present, the solution may exhibit only partial or superficial compatibility with other definitions. There are two cases to consider:
- Perfect prediction. If the feature space of the positive and negative class is cleanly separated with no overlap, then it is possible to satisfy both sufficiency and separation by developing an AI/ML classifier that learns to assign each individual to their correct class with certainty based on their respective features. In effect, this would lead to a model with predictive values of 1 and error rates of 0 across all groups.
- Equal base rates. If the fraction of members in the positive class is the same across all groups, then it is possible to satisfy all three definitions by simply assigning every individual to the positive class with a score equal to the base rate. While superficial in nature, such an AI/ML classifier would nonetheless ensure equality in terms of predictive values, error rates and proportionality of members in the positive and negative class across all groups. A more accurate, rigorous solution may be possible, but one is not guaranteed.Footnote 14
Conclusion
In this first part of our blog series on algorithmic fairness, we gained a number of insights into the history, context, nature and challenges of algorithmic fairness:
- Algorithmic fairness is an emerging field of research that arises when the future-oriented ambiguity of fairness meets the past-is-prologue precision of AI/ML
- As a type of fairness, it shares in the basic properties of the ethical concept of fairness:
- It involves recognition of both similarities and differences
- It has multiple standards
- The standards are generally incompatible
- In general, there are three main definitions of algorithmic fairness:
- Sufficiency or parity of predictive values
- Separation or parity of error rates
- Independence or statistical parity
- The definitions are generally incompatible due to an inherent trade-off between maximizing accuracy and minimizing differences among groups
- It is possible for some or all of the definitions to be satisfied simultaneously, albeit only in highly constrained special cases with trivial solutions
Based on these insights, it is clear that algorithmic fairness is a complex discipline. On the one hand, it offers useful mathematical definitions that create a framework for evaluating how our uses of AI/ML can be made more compatible with the idea of a fair and just society. Yet, at the same time, the general incompatibility of the definitions presents important challenges to practitioners. Many questions remain. For example, what measures can be applied to help achieve algorithmic fairness? How do we choose between definitions? What are the limits of mathematical notions of fairness?
Please continue to the second part of our blog series on algorithmic fairness, where we will discuss these questions and more.

